Ken Shirriff's blog

Reversing Sinclair's amazing 1974 calculator hack - half the ROM of the HP-35

In a hotel room in Texas, Clive Sinclair had a big problem. He wanted to sell a cheap scientific calculator that would grab the market from expensive calculators such as the popular HP-35. Hewlett-Packard had taken two years, 20 engineers, and a million dollars to design the HP-35, which used 5 complex chips and sold for $395. Sinclair's partnership with calculator manufacturer Bowmar had gone nowhere. Now Texas Instruments offered him an inexpensive calculator chip that could barely do four-function math. Could he use this chip to build a $100 scientific calculator?

Texas Instruments' engineers said this was impossible - their chip only had 3 storage registers, no subroutine calls, and no storage for constants such as π. The ROM storage in the calculator held only 320 instructions, just enough for basic arithmetic. How could they possibly squeeze any scientific functions into this chip?

Fortunately Clive Sinclair, head of Sinclair Radionics, had a secret weapon - programming whiz and math PhD Nigel Searle. In a few days in Texas, they came up with new algorithms and wrote the code for the world's first single-chip scientific calculator, somehow programming sine, cosine, tangent, arcsine, arccos, arctan, log, and exponentiation into the chip. The engineers at Texas Instruments were amazed.

How did they do it? Up until now it's been a mystery. But through reverse engineering, I've determined the exact algorithms and implemented a simulator that runs the calculator's actual code. The reverse-engineered code along with my detailed comments is in the window below.

											A register
											B register
											C register
											A flags
											B flags
											Mask / constant

Instr
Cond

Representing numbers

Numbers are represented as a 6-digit mantissa and a two-digit exponent. For example, 1234.5 has a mantissa of 1.2345 and an exponent of 3, so it is displayed as 1.2345 03. Interestingly, only 5 digits are displayed, although 6 digits are stored internally.

The mantissa and exponent each have a sign; positive is represented internally by the digit 0 and negative by the digit 5. This may seem random, but it actually makes sign arithmetic easy. For instance, when multiplying numbers the signs are added: positive times positive has 0+0=0 which indicates positive. Negative times negative has 5+5=0 indicating positive (the carry is dropped). Negative times positive has 5+0=5 indicating negative. This is one of the tricks that helps the Sinclair code fit into the small ROM.

It's slightly confusing that numbers are stored internally different from how they are displayed. The first digit in the A register is the mantissa sign, followed by the exponent sign. (The signs have to be stored in these locations since the hardware provides special display decoding for these digits which is how a 5 is displayed as a -.) The next two digits of the A register are the exponent, which is followed by the mantissa. This order is opposite from the display but makes some calculations simpler.

Limited performance and accuracy

The conceptual leap that made the Sinclair Scientific possible was realizing that many people didn't need the accuracy and performance of HP and TI calculators. (This can be considered an application of the Worse is Better design principle.) HP put a lot of work into the accuracy of the HP-35 calculator, using advanced transcendental pseudo-multiplication and pseudo-division algorithms (basically decimal CORDIC). The HP-35's scientific operations have from 7 to 11 digits of accuracy. In comparison, scientific operations on the Sinclair Scientific only have three decimal places of accuracy at best.

Due to the simple loop-based algorithms, the speed of the Sinclair Scientific calculator varies from good to horribly slow depending on the values. For instance, sin .1 takes under a second, but sin 1 takes about 7.5 seconds. Arccos .2 takes about 15 seconds. Log and antilog have the overhead of recomputing the constant 229.15, and take about 1 to 2 seconds. In comparison, the HP-35 was designed with a one second deadline for computations.

Using such slow, inaccurate algorithms would be unthinkable for HP or TI, but in the Sinclair Scientific they got the job done at a good price.

How the code fits into 320 words

The following chart shows how many instructions were used for different operations. Blue is the 4-function code that Texas Instruments originally wrote for the chip, and red is the Sinclair Scientific calculator code.

The category Function is code to read the keyboard input and keep track of what function is being performed. RPN greatly simplifies this, since functions are performed immediately. With algebraic notation, the calculator must store the function when it is entered, and then perform it later.

Using scientific notation shrunk the Sinclair Scientific's code in the next two categories: Digit is code to handle entering digits into a number and Display is code to format a number for display. As can be seen from the Texas Instrument code, a calculator with regular floating point numbers needs a lot of code to shift numbers back and forth and adjust the decimal point. In fact, since the Texas Instruments code ends up keeping an exponent internally, the floating point display is strictly overhead. Moving the minus sign to the correct display position is also overhead that the Sinclair Scientific avoids.

Normalize is the code to normalize the result of an operation and is fairly close on both calculators. The add/subtract/multiply/divide code is also similar length on both calculators. The scientific functions in the Sinclair Scientific fit into the remaining space. Trig functions were implemented in about 40 instructions. Arc-trig operations are almost 30 more instructions. Logarithms are about 40 instructions, with anti-log about 20 on top of that.

How addition and subtraction work

Addition and subtraction in the Sinclair Scientific are not too complicated. Since the two values may have different exponents, one of the values is shifted until the values line up. Then the mantissas are added or subtracted as appropriate. The code has some special cases to handle the different combinations of signs in the arguments.

After the operation (as with all operations) the result is normalized. That is, a result such as 0.0023 is shifted to 2.3000 and the exponent is correspondingly decreased by 3. Finally, registers are cleaned up and the result is displayed.

How multiplication works

You might be surprised to learn that the calculator chip cannot perform multiplication natively. There's no floating point unit to multiply two numbers. Instead, multiplication is performed through repeated addition, digit by digit. That is, the multiplicand is added the number of times in the low order digit of the multiplier. Then the multiplicand is multiplied by 10 and the multiplier is divided by 10 and the process repeats. The key trick is that multiplying and dividing by 10 are easy for the chip to do; the chip simply shifts the digits left or right.

For example, 23 * 34 is computed as 34 + 34 + 34 + 340 + 340 (i.e. 3 * 34 + 2 * 340).

Before multiplying the mantissas, the exponents are simply added. At the end, the result is normalized.

How division works

Division is done by repeated subtraction, somewhat like grade-school long division. First the divisor is normalized, since dividing by 0.0001 would be a lot of subtractions. Next, the exponents are subtracted. Finally, the divisor is subtracted as many times as possible, counting the number of subtractions into the result. The remainder is shifted and the process repeats through all the digits. For example, 7 ÷ 3 is computed as 7 - 3 - 3 counts 2 subtractions with remainder of 1, Shift the remainder to 10 and compute 10 - 3 - 3 - 3 counts 3 subtractions with a remainder of 1. This repeats a few more digits to generate the result 2.3333.

How trig operations work

How can sine and cosine be computed efficiently in a calculator that has a hard time even doing multiplication? The trick is to do repeated rotations by 0.001 radians until the desired angle is reached. If you have the cosine (C) and sine (S) for a particular angle, to rotate by .001 radians simply do:

C = C - S / 1000
S = S + C / 1000

These operations are quick and are done without division: S / 1000 is simply S shifted right three digits. (If you've studied graphics, this is basically a rotation matrix. This algorithm was discovered by Marvin Minsky and published in HAKMEM in 1972. I wonder if Sinclair read HAKMEM or rediscovered the algorithm.)

The calculator multiplies the input argument by 1000 (i.e. shifts it left three digits) and performs the rotation that many times; TRIGLOOP is the code that does this. At the end of the rotations, the sine and cosine are available. To compute the tangent, the sine and cosine are simply divided.

The following diagram illustrates. The starting unit vector (1, 0) is rotated in steps of .001 radian until angle θ is reached. At that point, the coordinates give cos θ and sin θ. (To be precise, the starting vector is (1, 0.0005) to provide rounding.)

While this algorithm requres very little code, it has the drawback of being very slow for large angles. Other calculators use algorithms such as decimal CORDIC that are much faster and more accurate, taking time proportional to the number of digits. But those algorithms are more complex and requires multiple constants during the computation.

Arcsine and arccosine use the same loop, but instead of iterating a fixed number of times, the rotation is performed until the sine or cosine of the vector matches the desired value, and the loop counter gives (after dividing by 1000) the angle θ, which is the desired arcsine or arccosine.

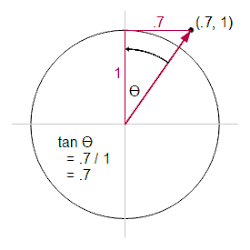
Arctan uses a slight modification. To compute arctan(z), the starting vector is (z, 1). The vector is rotated until vertical (the first coordinate is 0). The angle of rotation gives the arctan. The following diagram shows how this works for arctan(.7). Rotating the red vector by θ will make the x coordinate 0. tan(θ) is .7 (opposite ÷ adjacent in the red triangle). Thus, rotating the vector until it is vertical and counting to measure θ will generate the arctan.

How log works

Log and antilog are a bit more complicated than trig operations. The core of the calculation is computing powers of .99. This can be done efficiently in a loop, since X*.99 is X - X / 100, which is computed by just shifting the digits and subtracting.

The main log loop takes an input X and iterates through X*.99^N until the result is less than 1. The resulting loop counter N is approximately -log(X)/log(.99). By adding the remainder, a couple additional digits of accuracy are obtained - see the code comments for details.

One complication of using .99 as the base is the calculations require the constant 229.15 (which approximates -1/log(.99)) in several places. Unfortunately, the calculator can't store multi-digit constants. The solution is the calculator actually recomputes this constant every time it performs a log or antilog.

Putting this all together, the log is computed by using the loop to compute -log(10)/log(.99), which is the magic constant 229.15. The same loop is used on the mantissa of the input to compute -log(input)/log(.99). Dividing the two values yields the log of the input. Finally, the exponent of the input is simply added to the result, since log(10^N) is just N.

Thus, log is computed with a single slow division along with quick shifts, adds, and subtracts.

How antilog works

Antilog (i.e. 10^x) reuses much of the same code as log. The key observation for antilog is that 10^x = 10*.99^(229.15*(1-x)). To compute the antilog, first the magic constant 229.15 is computed as before. Next 1-x is multiplied by the constant. Then the powers of .99 loop is done that many times. Since the loop can only be done an integer number of times, a remainder is left over. To get more accuracy, a division is performed using the remainder - see the code for details.

Thus, antilog is computed with one multiplication, one division, and a lot of quick shifts, adds, and subtracts.

You might wonder how this algorithm can fit into three registers since there's the constant 229.15, the loop counter, the power of .99, and the power divided by 100, all in use at the same time. The trick is the registers are split in two. The chip's instructions support masks, so part of the register can be a counter and part can hold a computation value, for instance.

Sharing code and control flow

The diagram below shows the high-level control flow for the different operations the calculator performs. Note that multiple operations reuse the same code blocks. This is one way the code is squeezed into 320 words. Since the chip doesn't support subroutine calls, it's not as simple as just calling a multiply subroutine. Instead, the flag register is used to keep track of what's going on. For instance, at the end of multiplication, the control flow branches either to normalize or antilog based on one of the flags. Thus, flags and gotos are used as a replacement for subroutine calls.

Reverse engineering

The Visual 6502 group enjoys dissolving old chips in acid, photographing the die, and reverse-engineering them. I used their photo of the Sinclair Scientific chip to find out how the calculator works. It helped that I knew a lot about the Texas Instruments 080x chip architecture in advance since I'd written a TI calculator simulator. The image below shows a highly magnified image of the calculator chip with the main sections labeled. (The original image is here.) The chip is customizable, not just the instruction ROM, but also the operation masks, single-digit constants, display decoding, and even the instruction set! This allows the same basic chip to be easily modified for use in different calculators. For details on the operation of the chip, see my TI calculator simulator page with schematics and detailed explanation.

The image below zooms in on part of the ROM, showing individual transistors. The chip uses simple metal-gate PMOS technology. The vertical metal wires are clearly visible in the image. Underneath the metal is the silicon. Regions of the silicon have been modified to become conductive. In the ROM, these regions form horizontal conductors; the borders of the conductors are visible below. Finally, the rectangles in the image are the metal gates of transistors between two of the silicon lines. The larger rectangles are multiple transistors.

This chip uses simpler technology than chips such as the 6502. In particular, it doesn't have a layer of polysilicon interconnects like the 6502 processor.

The ROM is programmed by putting a transistor for a zero bit and omitting a transistor for a one bit. Once the layout of the ROM is known, reading the ROM is a simple matter of looking for transistors in the image. Likewise, the operation masks and single-digit constants can be figured out from the photograph. I converted the ROM contents into source code and wrote extensive comments explaining how the code works; the commented source code is displayed in the simulator window.

The Sinclair Scientific chip adds a couple instructions to the instruction set that weren't in the original chip. By looking at the instruction decoding circuit, it wasn't too hard to figure them out. The instructions were nothing special (for example, add A to B and store the result in C), but they probably made the code a few critical instructions shorter.

The image below shows the ALU instruction decode ROM. Each opcode from 31 to 0 has an input line on the top and is connected via transistors (the squares) to control lines that exit on the left. The ALU takes two arguments and by default performs addition. For instance opcode 0 is connected to "Arg1 is A", "Arg2 is B", and "Destination is A". Thus it adds A and B, putting the result in A. Opcode 13 selects C as argument 1, constant as argument 2, performs a subtract, and has no destination. Thus, it compares register C to a constant. Likewise, the other opcodes can easily be figured out from the image.

Bugs and limitations

The Sinclair Scientific cut a lot of corners to fit into 320 words of ROM, so it's not surprising there are problems. By looking at the code, we can see exactly what goes wrong.

The calculator manual specifies fairly restrictive limits on the allowable values for scientific operations, but the calculator doesn't enforce these limits. If you're outside the limits, there's no telling what the calculator might do. For instance, logarithm is only supported for arguments ≥ 1. The calculator almost works for arguments such as 5E-3, except it adds the exponent 3 instead of subtracting it, so the result is totally wrong. If they had room for just a few more instructions they could have made this work.

EdS found that 1.99996 antilog yields the wildly wrong answer of 0, even though it is in the supported antilog range. The problem is in the computation of 229.15*(1-.99996), the second factor is so small the multiplication yields 0 causing antilog to bail out.

The antilog code assumes that if the exponent is greater than 0, it is 1. Thus antilog of 0.01E2 yields 1.2589 instead of 10. Calling NORMALIZE would have fixed this, but there wasn't space for the call.

Arccos of a very small value (e.g. 0.0005) goes into an almost-infinite loop and takes 1 minute, 48 seconds to complete (as measured on a real calculator), before returning the wrong value 0. The root cause is since the angle is increased in steps of .001, it never exactly reaches the desired cosine value. When the rotation vector crosses vertical, the angle goes from 1.570 radians to 1.571 radians. cos 1.570 is bigger than .0005 so the loop doesn't exit. But at 1.571, everything falls apart: the loop uses unsigned arithmetic, so the sine value wraps to 999.99955 and the sine and cos become meaningless. The only reason the loop ever terminates is the loop counter eventually overflows after 9999 iterations, which inadvertently causes the code to fall into the arctan path and exit with 0.

Scientific calculators usually provide constants such as e and π but there was no space in the ROM for these constants. The Sinclair Scientific used the brilliant solution of printing the constants on the calculator's case - the user could enter the constant manually if needed.

Conclusions

The Sinclair Scientific came out in 1974 and was the first single-chip scientific calculator (if you ignore the display driver chips). It was stylishly compact, just 3/4 inch thick. It originally sold for the price of $119.95 or £49.95 and by the end of the year was available as a kit for the amazingly low price of £9.95.

Unfortunately, as calculator prices collapsed, so did Sinclair Radionics' profits, and the company was broken up in 1979 after heavy losses. Clive Sinclair's new company Sinclair Research went on to sell the highly-popular ZX 80 and ZX Spectrum home computers. Clive Sinclair was knighted for his accomplishments in 1983, becoming Sir Clive Sinclair.

Credits

This work was done in cooperation with the Visual 6502 team. Special thanks to John McMaster for chip processing and photography; Ed Spittles for timings and experiments on a real calculator, detailed feedback, and HAKMEM info; Phil Mainwaring for documentation, feedback and analysis; and James Abbatiello for code improvements. The Sinclair history is based on multiple sources including Electronics Weekly, Vintage Calculators, The Sinclair Story, and Programming the "Scientific" by Nigel Searle in Wireless World June 1974. The simulator is available on GitHub as TICalculatorJSSimulator.

If you want a short link to this page, use http://righto.com/sinclair.

This article has a bunch of interesting comments at Hackaday and Hacker News so take a look. Thanks for visiting!