Simulating a TI calculator with crazy 11-bit opcodes
To use the simulator, slowly click keys on the calculator image and you can watch how the calculator performs operations step by step. Since the processor doesn't do multiplication or division, it does these operations by repeated addition or subtraction. Try 2 ÷ 3 = for example.

| D | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | |||||||||||
| B | |||||||||||
| C | |||||||||||
| AF | |||||||||||
| BF | |||||||||||
| MASK/K | |||||||||||
| Instr | |||||||||||
| Cond | |||||||||||
The simulator
The simulator simulates the calculator at the register and instruction level, showing what the hardware really does. The register table at the bottom shows the digit scan register D, the 11-digit A, B, and C registers, the 11-bit flag registers AF and BF, the current mask and constant (K) value, the 11-bit instruction being executed, and the condition code. Above that, the display and keyboard matrix show how the hardware is organized and how one column of the display and keyboard gets scanned each operation. The source code window shows the code that is being executed. The A register hold the value that is displayed, and the B register controls the decimal point position.The simulator is implemented in JavaScript. I haven't optimized it for performance, since it's interesting to see the instructions as they execute. You can use the single-step button above the source window to see what's happening in more detail. For comparison, the real processor runs at about 4000 instructions per second.
Architecture
The TMS0800 series calculator chip was used in the TI-1500 calculator, Sinclair Scientific, and other calculators of the mid 1970s. This processor has many unusual architectural features. It's interesting to examine this chip and discover how many CPU features that we take for granted can actually be done very differently.The three registers (A, B, and C) hold eleven decimal digits as BCD, and the arithmetic takes place in decimal, digit by digit. The chip supports multi-digit decimal addition and subtraction, but not multiplication or division.
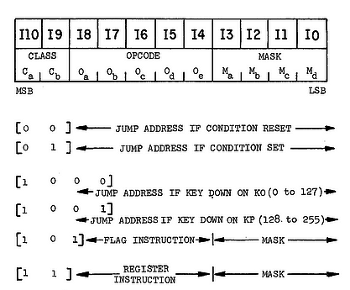
Each instruction is an 11 bit opcode, which comes from a ROM that has 320 11-bit words. The entire calculator software had to fit in this tiny ROM. An eleven bit instruction set seems very unusual, but it allows all instructions to fit into a single 11-bit word, avoiding multi-byte instructions. The first two bits of an instruction are the "class", selecting the type of instruction (arithmetic, flag, or branch). The next 5 bits select the specific instruction opcode. The final four bits select the mask and constant. The following drawing from the patent shows the structure:
The instructions are fairly basic, such as AABA, which adds A and B storing to A, or SRLA, which shifts register A left by one digit. If you single-step using the control above the source window, each instruction is explained in more detail.
One of the most unusual features of this processor is that operations have a mask that selects which digits are affected. For instance, when adding the A and B registers, a single digit can be added, all 11 digits can be added, or the two highest digits can be added depending on the mask specified in the instruction. Likewise, an operation can act on a single flag, the three lowest flags, or other combinations. In total, there are 16 different masks. This gives the processor a lot of flexibility, and allows a single operation to process multiple digits without coding a loop - the hardware does the loop internally.
The mask bits also select a constant value associated with a mask. For instance, the lowest digit can be incremented by 7 or the second digit can be incremented by 4, or 0 can be stored into all the digits, depending on the mask in the instruction. Most processors use a second instruction word to specify constant values, but the TI processor folds the constants into the single instruction. The full list of masks and constants is here.
The two 11-bit flag registers AF and BF are a very important part of the processor, as they are used to keep track of the calculator's state. For instance, the calculator remembers which operation key was pressed by using a few flag bits. The set, clear, test, compare, and exchange operations are also controlled by the mask, so they can operate on a single bit or multiple bits at a time. Boolean operations are notably missing.
One feature of the chip specially designed for calculators is the digit scan register, which cycles through 10 scan lines. These lines illuminate one digit at a time. They also scan the key matrix to detect key presses. Several of the instructions are tied closely to the digit scan. For instance, AKCN increments A each scan until a key is found. Since keys 1 through 9 and tied to scan lines 1 through 9, the result is the desired digit value. Similarly SYNC synchronizes execution to the scan.
The chip has a single condition bit. Depending on the instruction, this holds the status for key down, carry, borrow, equality, or zero. Most processors use separate condition flags for each type of condition. In contrast, t 0800 has a single flag and the programmer needs to keep track of what it holds. The condition flag is used to control conditional branches. There is no unconditional branch - the BET (branch every time) instruction is just a condition branch when the programmer knows the condition flag is clear. The top two class bits indicate a conditional branch, leaving 9 bits for the address. Thus, branch instructions fit in a single word, unlike most processors.
A few instructions don't have room for an opcode and branch address, so they use the same bits for both, which is very strange. The WAITNO and WAITDK instructions branch when a key is pressed. The bizarre thing about these instructions is that the opcode takes up most of the address bits, so there is little choice about where the branch ends up. The destination instruction is forced to go in a small area, even if that's in the middle of an unrelated block of code.
If you want to know more about the chip, the architecture diagram from the patent and the chip schematic links below are extremely detailed. I tediously assembled the schematic from many pieces in the patent.
Algorithms
The chip patent includes the full source code for the calculator, implementing addition, subtraction, multiplication, and division. The chip doesn't support multiplication or division directly so multiplication is performed by repeated addition, and division is performed by repeated subtraction, very similar to grade-school multiplication and long division.During computation, numbers are represented as a sign flag, a 9-digit mantissa, and a 2 digit exponent. The exponent indicates how many digits are after the decimal point. e.g. 1.23 has a mantissa of 123 and an exponent of 2. Numbers are shifted left and aligned during computation so 1.23 can also be represented mantissa 12300000 and exponent 7. You can see the numbers getting shifted left and right during computation.
For display, the A register holds the sign (represented by the number 14) and the displayed digits. The B register indicates the position of the decimal point by having the digit 2 at the decimal point position. A minus sign is indicated by the digit value 14 in A at the proper position. Leading zeros are suppressed by the hardware, so for instance it displays 12, not 000000012.
I've added extensive comments to the source code.
As an outline of the code, it starts with CLEAR, which resets everything. The LOCK loop waits for keys to get released, and then IDLE waits for a key press. KEY waits a bit to debounce the key and then scans for a non-digit key. Then it counts the scans to get the value of any digit key. A digit is appended to A and then DPTPOS sets B to display the decimal point correctly.
To perform addition or subtraction, the two arguments are aligned along their decimal points, added or subtracted, and the sign set appropriately. Multiplication is done by repeatedly adding, multiplying by 10, and continuing through all the digits. Division is done by repeatedly subtracting, multiplying by 10, and continuing through all the digits. After the operation, the POST code normalizes the result and handles any overflow.
Additional code handles constant operations, a more advanced feature than you'd expect to find in a simple calculator. E.g. if you enter "3 * 6 = ", followed by "9 =", the calculator remembers the previous "* 6" operation and computes "9 * 6". (Sort of currying.) The constant mantissa is stored in C, the exponent is stored in B, and the operation is stored in the AF flags. Likewise, "5 * = = " computes 5 cubed.
It's interesting to watch the digits bounce back and forth, even for simple computations. There's a lot more happening in a calculator and more programming involved than you might think.
After a divide by zero or overflow, the calculator will lock up until you hit Clear. I thought earlier that there was a bug in the original source code that kept Clear from working, but it turns out that the Clear button is actually wired in the calculator to the hardware reset, rather than being implemented in the code. I added this reset feature to the simulator and Clear now works.
Making a scientific calculator from this chip
The most amazing thing about this chip is that the Sinclair company took this chip with barely enough ROM to do four-function math, and reprogrammed it into a scientific calculator with trig, inverse trig, exponentials, and logs. The resulting Sinclair Scientific calculator became popular due to its low cost.How did Sinclair fit all this into 320 words of ROM? The short answer is they used RPN which simplified the code, and they made extreme tradeoffs in the scientific algorithms that reduced accuracy and performance. The algorithms are a bit like decimal CORDIC, but much simplified. I plan to provide full details later.
Notes and credits
For sharing, righto.com/ti is a short link to this page.This simulator is based on the extremely detailed 50 page patent (3934233), which is one of the most informative patents I've seen. I wish all patents were like this one: the text seems to have been written by engineers who wanted to explain everything, and the patent includes the full schematic and source code. Ironically, the patent itself is very narrow, claiming an obscure detail of the ROM decoding that could have been written up in about 2 pages.
Source code entered by Phil Mainwaring. Calculator image from Ralf Pfeifer at de.wikipedia. Built using jQuery and tested with QUnit. Inspired by Visual 6502.
Random cultural reference: This TI calculator also appears on the cover of Zero Day by nerdcore artist MC Frontalot.